15 de març 2024

BIBLIOTECA DEL MÓN ANTIC: Eratòstenes: la mesura de la Terra (S. III - II aC)

Ciències Socials de 1r d'ESO
Biblioteca del món antic - Grècia i l'Egipte hel·lenístic
SA7. Del bronze al ferro: Grècia i l'origen de la democràcia

Ja sabem per la biografia d'Eratòstenes que era un savi que va investigar i escriure sobre molts temes. Entre molts altres temes, va destacar en l'aplicació de principis matemàtics, i sobretot, geomètrics, a la Geografia. És autor d'una obra que tenia per títol Geografia i que hauria anat precedit d'un tractat amb el títol de Sobre la mesura de la Terra on parlava d'eclipsis, de les distàncies al Sol i la Lluna i de la grandària d'aquests astres i, assenyaladament, de la seva recerca sobra les mesures de la circumferència de la Terra. Aquesta obra s'ha perdut però se'n conserven fragments o resums en obres d'altres autors, com Estrabó o Cleòmedes.

Eratòstenes va disposar de força recursos per construir instruments per a la seva recerca, com ara armil·les i gnòmons.

Una armil·la o esfera armil·lar és un instruments astronòmic format per cercles, que, a Grècia, se n'atribueix la invenció al propi Eratòstenes, si bé sembla que a la Xina inventaren instruments semblants dos segles abans. Al centre es situa la Terra i al seu voltant es disposen diferents cèrcols articulats que representen el moviment aparent dels astres. 

Imatge: una esfera armil·lar (Viquipèdia)

Els gnòmons, per altra banda, són també instruments astronòmics que, amb l'ombra que produeixen, permeten de visualitzar el desplaçament del sol. En la seva forma més simple consisteixen en un pal o estaca que es clava verticalment en un lloc assolellat.

El major èxit que s'atribueix a Eratòstenes és el càlcul de la circumferència de la Terra. Com que ja hem dit que l'obra original s'ha perdut, cal recórrer a altres autors i, en aquest cas, a Cleòmedes, que va resumir molt bé els supòsits i el procediment d'Eratòstenes.

De la vida de Cleòmedes no en sabem res de res, ni tan sols quan va viure, i només podem suposar que ho va fer en algun moment entre la meitat del segle I. aC i finals del segle II dC. si bé també se l'ha situat a finals del S. IV dC. En tot cas, d'ell s'ha conservat una obra que porta per títol Els Cels i que va ser conegut a l'època moderna com De motu circulari corporum celestium (Sobre el moviment circular dels cossos celestes). En aquesta obra va incloure una explicació de la demostració d'Eratòstenes sobre la circumferència de la Terra.

Al costat, una edició grega i llatina de 1547 de l'obra de Cleòmedes, al paràgraf on comença a explicar l'obra d'Eratòstenes, a la pàgina 160 (font: Biblioteca Virtual Miguel de Cervantes en un volum que inclou diferents obres sobre l'univers).

Cleòmedes primer presenta els supòsits bàsics d'Eratòstenes i després n'explica el raonament. 

L'edició que fem servir: traducció i adaptació pròpies de les edicions disponibles, citades a la bibliografia, amb l'ajut d'alguns articles científics també citats. Oferim dues versions, la primera, molt sintètica i molt adaptada, i que és la més adequada per treballar a classe, i la segona, més literal i més complexa. En els dos casos, el text de Cleòmedes és en color marró.

Versió 1

Mirem com ho va fer Eratòstenes i rumiem quins recursos (materials o de coneixements de l'època) devia fer servir per obtenir els seus resultats.

El mètode d'Eratòstenes depèn d'un argument geomètric, i dona la impressió de ser difícil d'entendre. Però el seu punt de vista es veurà més clar si seguim el seu raonament amb atenció.

Siena i Alexandria, diu Eratòstenes, estan situades en el mateix meridià. 

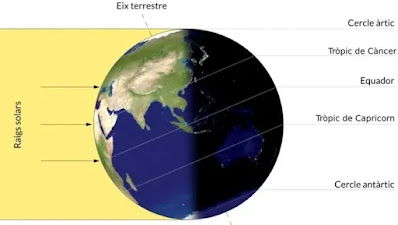
Diu Eratòstenes que Siena està situada en el tròpic d’estiu [o sigui, el Tròpic de Càncer]. Per tant, quan allà es produeix el solstici d’estiu, el sol es troba al mig del cel i els gnòmons dels rellotges solars no fan cap mena d’ombra ja que la posició del cel sobre ells és del tot vertical, i això és així en un espai d’uns 300 estadis de diàmetre. Però a Alexandria, a la mateixa hora, els gnòmons dels rellotges solars fan ombra, ja que Alexandria es troba més al nord que Siena.

Ja hem dit que els gnòmons són també instruments astronòmics que, amb l'ombra que produeixen, permeten de visualitzar el desplaçament del sol. En la seva forma més simple consisteixen en un pal o estaca que es clava verticalment en un lloc assolellat. 

A la imatge, un rellotge de sol hemisfèric o Skaphe, que era l'usat a Grècia per a conèixer l'hora, i que, molt probablement, va ser el que va fer servir Eratòstenes per veure les ombres de les dues ciutats, amb el seu gnòmon, o vareta o tija vertical. Efectivament, per tal que els gnòmons dels rellotges no fessin ombra quan al migdia del solstici d'estiu el sol es trobava al zenit, o sigui a la seva vertical, el rellotge havia de ser horitzontal. 

La imatge de la Terra durant el solstici d'estiu procedeix de Néstor Gómez, "Dades curioses i poc conegudes del solstici d'estiu", 3Cat, El temps, 19/6/2019 i 8/9/2020; l'Skaphe grec procedeix del Museu Clemens - Sels de la ciutat alemanya de Neuss (Imatge: Viquipèdia).

En un rellotge de sol situat en un lloc determinat el moviment de l'ombra indica el pas del dia. En canvi, si mirem dos rellotges situats en un mateix meridià a la mateixa hora, la diferència de situació de l'ombra indica la diferent latitud, com ja havia establert Piteas de Marsella (un altre geògraf que va viure aproximadament vora el voltant el 320 aC.).

El que cal ara, per tant, és mesurar l'angle de l'ombra del rellotge d'Alexandria.

  • Si el voleu calcular com ho va fer Eratòstenes, aleshores heu de seguir les instruccions que ens donen Lorenzo Ramírez o Inmaculada Cuadrado. 
  • Però si el que us interessa és, sobretot, el procediment concret de mesura de l'angle i el conjunt de recursos que Eratòstenes va mobilitzar, aleshores ho podeu fer en qualsevol moment (i usar per als càlculs les dades del savi, és clar).
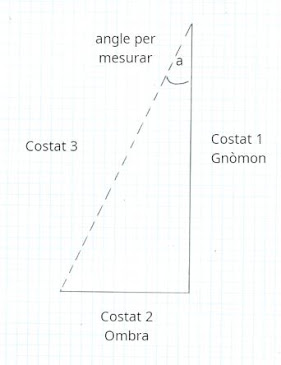
  • Per mesurar aquest angle es pot dibuixar un triangle. El costat o catet 1 seria el pal o gnòmon de rellotge que projectava l'ombra; el costat o catet 2 seria l'ombra, i el costat 3 seria la hipotenusa que uniria els altres dos. L'angle a mesurar seria l'angle superior, dibuixat pels costats 1 i 3. 
  • Eratòstenes va mesurar el seu angle i el resultat va ser de 7º 12' o 7,2º. A Siena el valor era 0º (no feia ombra perquè es trobava a la vertical del sol) i per tant, la dada que tenia el nostre savi era, per a la mateixa longitud (les dues poblacions eren, gairebé, a sobre del mateix meridià) la diferència de latitud.

Ara bé, com ho va fer per passar dels 7,2º de l'angle de la nostra ombra a poder calcular les dimensions de la circumferència de la Terra?

Ho va fer amb una aplicació del postul·lat de la geometria d'Euclides (un matemàtic que va viure al voltant del 300 aC) que diu que "si dues rectes paral·leles es tallen per una tercera recta, els angles alterns interns que es formen són iguals", com es veu a l'esquema següent (elaboració pròpia):

Si imaginem unes rectes que travessen la Terra a partir de cadascun dels gnòmons, ambdues rectes es trobaran al centre de la Terra [són les línies 1, la de Siena, i 2, la d’Alexandria]. Com que el rellotge de sol de Siena és a la vertical del Sol, si imaginem una línia recta que surt del Sol i arriba a la punta del gnòmon del rellotge, aquesta línia recta sortirà del Sol i arribarà al centre de la Terra [es refereix un altre cop a la línia 1]. 

I si imaginem una altra línia recta que surti de l’extrem de l’ombra del gnòmon d’Alexandria i uneixi la punta d’aquest gnòmon amb el Sol [línia 3], aquesta línia i la de Siena [línia 1] seran paral·leles.

Aquestes línies paral·leles són tallades per la recta que va del centre de la Terra fins al gnòmon d’Alexandria [línia 2], formant angles alterns iguals, el primer dels quals [angle a] se situa al centre de la Terra, en la intersecció de les rectes que hem traçat des dels rellotges fins al Centre de la Terra [línies 1 i 2], i el segon [angle b] se situa en la intersecció del gnòmon d’Alexandria i la recta traçada des de l’extrem de la seva ombra fins al Sol [línies 2 i 3] passant pel seu punt de contacte amb el gnòmon.

Aleshores, si això era així, si una esfera són 360º i l'angle interior són 7º 12', aquest angle és aproximadament 1/50 part de tota l'esfera. Per tant, l'arc circular que es dibuixa entre Siena i Alexandria també serà 1/50 part de la circumferència de tota la Terra. Cal mesurar la distància entre les dues ciutats per obtenir, amb una multiplicació, el que mesura la circumferència de la Terra.

La distància entre Siena i Alexandria és de 5.000 estadis. El cercle en la seva totalitat mesura, per tant, 250.000 estadis. Heus aquí el mètode d'Eratòstenes.

Cal tenir en compte que l'estadi, com a mesura de longitud, no era igual arreu. L'estadi olímpic, per exemple, mesurava uns 192 metres, mentre que l'estadi dels Ptolomeus en mesurava uns 157,5. Si fem servir aquesta darrera mesura, la distància entre Siena i Alexandria seria de 787,5 km i les dimensions de la circumferència de la Terra segons Eratòstenes serien de 39.375 km, que seria una aproximació molt remarcable, ja que la real és de 40.074 km. 


Ara que ja hem vist tot el raonament:

  • Recull el conjunt de recursos materials i intel·lectuals que va fer servir Eratòstenes per assolir el seu objectiu
  • Valora els seus resultats. Què et sembla que algú pugui mesurar quelcom i que no es pugui comprovar fins molts anys després, i que, tanmateix, tingui raó ?
  • Amb el google maps mesurarem la distància entre Alexandria i Siena (Assuan). Quin resultat et dona?
  • També podem fer servir la diferència d'ombres entre Alexandria i Siena com a argument per defensar que la Terra és una esfera. Mireu els primers 10 minuts d'aquest Què Qui Com


Versió 2. Textos de Cleòmedes en marró i comentaris en negre.

Comencem, com hem dit, pels supòsits d'Eratòstenes.

El mètode d'Eratòstenes depèn d'un argument geomètric, i dona la impressió de ser més difícil d'entendre (que l'argument de Posidoni). Però el seu punt de vista es veurà més clar si admetem els supòsits següents. Suposem, primer, que Siena i Alexandria es troben al mateix cercle meridià. En segon lloc, que la distància entre les dues ciutats és de 5.000 estadis. En tercer lloc, que els raigs del sol que arriben a la Terra són paral·lels, fet que és assumit pels geòmetres. En quart lloc, suposem, com demostren els geòmetres, que les rectes que tallen rectes paral·leles formen angles alterns siguin iguals. En cinquè lloc, que els arcs de cercle que reposen sobre angles iguals seran semblants, fet demostrat també pels geòmetres. Per tant, sempre que els arcs de cercles es basin en angles iguals, si algun d'aquests arcs és (per exemple) una desena part del seu cercle, tots els altres arcs seran desenes parts dels seus propis cercles.

I analitzem ara el raonament.

1. Siena i Alexandria estan situades sobre el mateix meridià

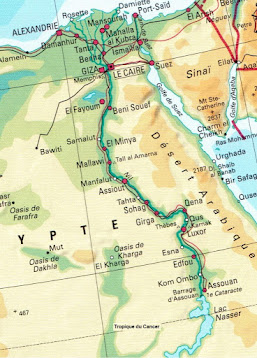
Siena i Alexandria, diu Eratòstenes, estan situades en el mateix meridià. 

Mira el mapa del costat (mapa procedent de Philippe Cibois (2019)). Si l'antiga Siena estava situada on avui hi ha Assuan, es pot dir que les dues ciutats estaven situades exactament sobre el mateix meridià?

Com que els meridians són els cercles més grans de l’univers, els cercles de la terra que hi ha sota d'ells també són necessàriament grans cercles. I, per tant, el cercle de la terra que passi per Siena i Alexandria serà la mida del gran cercle de la terra. 

Mira l'esfera armil·lar reproduïda més amunt. A què et sembla que es refereix l'autor quan parla dels "cercles de l'univers" sota dels quals hi ha els "cercles de la terra"? Quina imatge dels meridians suggereix això?

2. A Siena i a Alexandria l'ombra dels rellotges no és igual

Diu també Eratòstenes que Siena està situada en el tròpic d’estiu. Per tant, quan allà es produeix el solstici d’estiu, el sol es troba al mig del cel i els gnòmons dels rellotges solars no fan cap mena d’ombra ja que la posició del cel sobre ells és del tot vertical, i això és així en un espai d’uns 300 estadis de diàmetre. Però a Alexandria, a la mateixa hora, els gnòmons dels rellotges solars fan ombra, ja que Alexandria es troba més al nord que Siena.

Si el "tròpic d'estiu" és el Tròpic de Càncer, Siena està situada sobre aquesta línia imaginària o només ho està aproximadament?

Recordem què és el solstici d'estiu, i com arriben els raigs de sol a la Terra en aquesta data.
"Els solsticis marquen el pas de la tardor a l'hivern i de la primavera a l'estiu. Tenen lloc pels volts del 21 de desembre (solstici d'hivern) i el 21 de juny (solstici d'estiu), respectivament, quan els rajos del Sol arriben de manera perpendicular a un dels tròpics i incideixen molt més sobre un hemisferi que sobre un altre" (Llibre de text Santillana) (Imatge: la Terra durant el solstici d'estiu (Font: Néstor Gómez, "Dades curioses i poc conegudes del solstici d'estiu", 3Cat, El temps, 19/6/2019 i 8/9/2020)
Fixa't en el rellotge de sol que tens al costat. És un rellotge semblant, dit rellotge de sol hemisfèric o skaphe, que era l'usat a Grècia per a conèixer l'hora, i devia ser d'aquest tipus el que, molt probablement, va fer servir Eratòstenes per veure les ombres de les dues ciutats, amb el seu gnòmon, o vareta o tija vertical. Per tal que els gnòmons dels rellotges no fessin ombra quan al migdia del solstici d'estiu el sol es trobava al zenit, o sigui a la seva vertical, el rellotge havia de ser horitzontal. 

Museu Clemens - Sels (Imatge: Viquipèdia).

En un rellotge de sol situat en un lloc determinat el moviment de l'ombra indica el pas del dia.

En canvi, si mirem dos rellotges situats en un mateix meridià a la mateixa hora, la diferència de situació de l'ombra indica la diferent latitud.

  • De la latitud, ja n'hem parlat als temes de geografia. Recordem, primer, que la latitud és _____________________________
  • De la latitud també n'hem parlat en el tema dels climes, de manera que ja sabem que a mesura que augmenta la latitud la temperatura________________ a causa que va canviant la ____________ dels raigs del sol que arriben a la terra, o sigui, que els raigs del sol no arriben a la Terra amb el mateix angle.
  • Si apliquem la latitud al rellotge, és conegut que la diferència de latitud condiciona les ombres que produeix un rellotge de sol, i que, per tant, el rellotge ha d'estar adequat a la seva situació geogràfica. La diferència d'ombres a la mateixa hora entre dos rellotges situats en dos llocs diferents situats a la mateixa longitud pot ser mesurada amb un angle, i això és el que va permetre a Eratòstenes de calcular les dimensions de la Terra.

A Siena, el rellotge d'Eratòstenes no feia ombra, i a Alexandria, sí, per tant, el primer que ens cal és mesurar l'angle de l'ombra del rellotge d'Alexandria.
  • Si el voleu calcular com ho va fer Eratòstenes, aleshores heu de seguir les instruccions que ens donen Lorenzo Ramírez o Inmaculada Cuadrado. 
  • Però si el que us interessa és, sobretot, el procediment concret de mesura de l'angle i el conjunt de recursos que Eratòstenes va mobilitzar, aleshores ho podeu fer en qualsevol moment (i usar per als càlculs les dades del savi, és clar).
  • Per mesurar aquest angle es pot dibuixar un triangle. El costat o catet 1 seria el pal o gnòmon de rellotge que projectava l'ombra; el costat o catet 2 seria l'ombra, i el costat 3 seri la hipotenusa que uniria els altres dos. L'angle a mesurar seria l'angle superior, dibuixat pels costats 1 i 3. 
  • Eratòstenes va mesurar el seu angle i el resultat va ser de 7º 12' o 7,2º. A Siena el valor era 0º (no feia ombra perquè es trobava a la vertical del sol) i per tant, la dada que tenia el nostre savi era, per a la mateixa longitud (les dues poblacions eren, gairebé, a sobre del mateix meridià) la diferència de latitud.

Fixeu-vos que amb tot això, Eratòstenes ja donava per descomptat que la Terra era rodona. La diferència d'ombres és un argument més a favor, com podem veure als primers 10 minuts del video següent del Què Qui Com:

 
3. Aquest angle ens serveix per esbrinar les dimensions de la Terra.

En primer lloc, cal tenir en compte aquell postul·lat de la geometria que diu que "si dues rectes paral·leles es tallen per una tercera recta, els angles alterns interns que es formen són iguals". El cas de les dimensions de la Terra és una aplicació pràctica d'aquest postul·lat (afegeixo referències a les línies imaginàries que ell traça per identificar-les al dibuix que he fet per il·lustrar-ho).

Si imaginem unes rectes que travessen la Terra a partir de cadascun dels gnòmons, ambdues rectes es trobaran al centre de la Terra [són les línies 1, la de Siena, i 2, la d’Alexandria]. Com que el rellotge de sol de Siena és a la vertical del Sol, si imaginem una línia recta que surt del Sol i arriba a la punta del gnòmon del rellotge, aquesta línia recta sortirà del Sol i arribarà al centre de la Terra [es refereix un altre cop a la línia 1]. 

I si imaginem una altra línia recta que surti de l’extrem de l’ombra del gnòmon d’Alexandria i uneixi la punta d’aquest gnòmon amb el Sol [línia 3], aquesta línia i la de Siena [línia 1] seran paral·leles.

Aquestes línies paral·leles són tallades per la recta que va del centre de la Terra fins al gnòmon d’Alexandria [línia 2], formant angles alterns iguals, el primer dels quals [angle a] se situa al centre de la Terra, en la intersecció de les rectes que hem traçat des dels rellotges fins al Centre de la Terra [línies 1 i 2], i el segon [angle b] se situa en la intersecció del gnòmon d’Alexandria i la recta traçada des de l’extrem de la seva ombra fins al Sol [línies 2 i 3] passant pel seu punt de contacte amb el gnòmon.

Òbviament, l'angle del cercle de la Terra no pot ser mesurat físicament, però sí que podia ser mesurat el del rellotge, com ja hem vist. 

A continuació, Cleòmedes explica que sobre els angles esmentats reposen arcs de cercle que també podran ser mesurats.

Un arc de cercle o arc circular és un segment de circumferència d'un cercle, delimitat per dos punts (esquema: Viquipèdia).

Sobre l’angle mesurat a Alexandria [angle b], reposa l’arc de cercle que va de l’extrem de l’ombra del gnòmon a la seva base, mentre que sobre l’altre angle [angle a], que és al centre de la Terra, reposa l’arc que va de Siena a Alexandria. Aquests arcs de cercle són, per tant, semblants entre sí perquè estan construïts sobre angles iguals.

Que siguin semblants vol dir que la proporció que guarden amb el conjunt del seu cercle és la mateixa, com diu tot seguit:

La relació que hi ha entre l'arc circular del rellotge i el seu cercle és igual a la relació que hi ha per a l'arc de cercle que va de Siena a Alexandria. Així, trobem que l'arc del rellotge és la cinquentena part del seu cercle. Cal, per tant, que la distància que hi ha entre Siena i Alexandria sigui la cinquentena part del cercle més gran de la Terra [o sigui, del meridià]

El que està dient Cleòmedes és que, en la mesura que l'angle mesurat al seu rellotge d'Alexandria és de 7,2º, l'angle de la Terra també tindrà la mateixa mesura i ambdós suposaran 1/50 part de les seves esferes, ja que una esfera mesura 360º (l'angle del centre de la Terra es referirà a l'esfera terrestre i l'angle del rellotge a una esfera imaginària que es podria dibuixar al seu voltant). I com que els angles són 1/50 part, els arcs circulars també seran 1/50 part de les seves circumferències. Si es pot mesurar la distància entre Siena i Alexandria, aquesta distància serà 1/50 part de tota la circumferència terrestre. 

Font de les imatges: Philippe Cibois (2019)

















Finalment, només resta aplicar la distància entre Siena i Alexandria per obtenir la mesura de la circumferència de la Terra:
La distància entre Siena i Alexandria és de 5.000 estadis. El cercle en la seva totalitat mesura, per tant, 250.000 estadis. Heus aquí el mètode d'Eratòstenes. 
Eratòstenes devia ser molt meticulós perquè va repetir l'experiment durant el solstici d'hivern, amb el mateix resultat, si bé en aquest cas cap angle és igual a 0 i, per tant, cal fer una resta d'angles.
Eratòstenes va col·locar rellotges solars a cadascuna de les dues ciutats durant el solstici d'hivern. L'ombra d'Alexandria era més llarga, ja que aquesta ciutat està més allunyada del tròpic d'hivern [o Tròpic de Capricorni]. Si veiem la diferència d'ombres entre Siena i Alexadria, trobem que aquesta diferència també correspon a la cinquantena part del cercle major dels rellotges. A partir d'aquests càlculs sabem també que la circumferència més gran de la Terra mesura 250.000 estadis.
Eratòstenes també va calcular el diàmetre de la Terra:
El diàmetre de la Terra mesurarà, per tant, més de 80.000 estadis, ja que ha de ser igual a la tercera part del cercle més gran.
Efectivament, el diàmetre és aproximadament una tercera part de la seva circumferència, ja que 

d= C/π   o    r = C/(2π)

on:
  • d: diàmetre
  • C. circumferència
  • r: radi


_______________________________________________________________

Versions del text de Cleòmedes
  • en grec i llatí: Procli de Sphaera liber / [Thoma Linacro interprete]. Cleomedis de Mundo... libri duo [Georgio Valla interprete]. Arati Solensis Phaenomena sive Apparentia. Dionysii Afri descriptio orbis habitabilis ; Omnia graece et latine ... coniuncta ... adiectis etiam annotationibus, Basileae, per Henricum Petri, 1547, p.160-169
  • en francès (referència fonamental per a una bona comprensió del text): Nicolas Decamp i Cécile de Hosson, "Quelqueséléments historiques et didactiques sur l’expérienced’Ératosthène". Bulletin de l’Union des Physiciens, vol 105, oct 2011
  • en castellà: pàgina web de Vernor Arguedas (Escuela de Matemáticas, U de Costa Rica); consultat el 15/3/24, en aquest moment la traducció té un error greu, ja que diu que l'angle i l'arc circular són una cinquena part dels seus cercles, quan hauria de dir cinquentena part.
  • en anglès: bloc de Roger Pearse


Altra bibliografia:


a